Home » Examen oefeningen » Start pagina F/C examens » Full Exameneisen » Inleiding » Wiskunde

Optellen, aftrekken, vermenigvuldigen en delen

Bij het rekenen dient men de volorde waarin gewerkt moet, goed in de gaten te houden. Hiervoor is een ezelsbruggetje; Meneer Van Dale Wacht Op Antwoord. Van boven naar beneden is de volgorde van verwerking.

• M - machtsverheffen
• V - vermenigvuldigen
• D - delen
• W - worteltrekken
• O - optellen
• A - aftrekken

Wordt van bovenstaande volgorde afgeweken wordt dit altijd aangegeven door dit te plaatsen tussen {},() en of [].

Gehele waarden, omgekeerde waarden, breuken

Hele getallen zijn 1, 2, 5 10 etc.

Gehele waarden versus omgekeerde waarden;

$$ a = { 1 \over a } $$

, hierbij is $$ { 1 \over a} $$ de omgekeerde waarde van a.

Voor a mag elk geheel getal worden ingevuld.

Gebrokken getallen zijn;

$$ { 1 \over 2} , { 1 \over 4 } , {1 \over 8} $$

etc.

Het getal boven de breukstreep wordt de teller genoemd, het getal onder de streep de noemer. De waarde van een breuk verandert niet wanner men de teller en de noemer hetzelfde getal deelt of vermenigvuldigt.

Voorbeelden:

$$ { 3 \over 4} = { 3 * 4 \over 4 * 4 } = {12 \over 16} $$

$$ { 12 \over 16} = { 12 : 4 \over 16 : 4 } = {3 \over 4} $$

Breuken dient men gelijknamig te kunnen maken, te vermenigvuldigen en te kunnen delen.

Percentage

Procent (of percent) betekend per 100 (=gedeeld door 100) , het teken is %.

1/100 of

$$ { 1 \over 100 } $$

= 0,01 = 1%.

Machtensverheffen, kwadrateren

Voorbeelden: 3², 2⁶, 10³ ;

3² = 3 * 3 = 9 (3 tot de 2e macht, of 3 kwadraat)
2⁶ = 2 * 2 * 2 * 2 * 2 * 2 * 2 = 64
10³ = 10 * 10 * 10 = 1000

Van 10³ is 10 het grondtal en 3 de exponent.

Exponenten

Om hele grote of hele kleine getallen te kunnen schrijven worden ze vermenigvuldigd met de macht van 10.

Voorbeelden;

56200 = 5,62 X 10⁴
De komma is 4 plaatsen naar links geschoven. Dit wordt ook geschreven als 5,62E4

Vierkantswortels (worteltrekken)

Zoals delen het omgekeerde is van vermenigvuldigen, is het worteltrekken het omgekeerde van machtsverheffen. $$ a^{1/2} = \sqrt a $$ Bij het wortel trekken is de exponent geen geheel getal zoals bij het machtsverheffen. Het zijn breuken. Om het oorspronkelijke getal uit een wortel te krijgen, wordt deze met zich zelf gekwadrateerd. $$ \sqrt 4 = \sqrt {2^{1/2}} = 2 $$ Voor de zend amateur is het handig om de onderstaande wortels te kennen, deze komen veel voor in formules:

$$ \sqrt 2 = 1,41 $$

en $$ \sqrt 3 = 1,73 $$

Logaritmen

Een logaritme is het tegenovergestelde van een exponent. Met een logaritme kun je de exponent berekenen. Als men log a schrijft dan, dan wordt daar mee altijd het grondtal 10 bedoeld. Log 100 is 10, want 10² is 100.

In onderstaand voorbeeld is 2 het grondtal, tussen haakjes het getal van het machtsverheffen resultaat (van het grondtal).

$$ log_2(8) = 3 $$

want $$ 2^3 = 8 $$

Volgend voorbeeld is identiek alleen de schrijfwijze is anders.

$$ ^2log(8) = 3 $$

want $$ 2^3 = 8 $$

Om te kunnen rekenen met logaritmes zijn de volgden formules van belang. $$ log(a) + log(b) = log(a*b) $$ $$ log(a) – log(b) = log(a/b) $$ De meest voorkomende grontallen zijn 10,2 en e. Het logaritme met als grontal e is een bijzondere en deze wordt het natuurlijke logaritme genoemd. Het heeft als waarde ongeveer 2,718.

De schrijfwijze is

$$ ln(x) $$

ipv $$ log_e(x) $$

Als het grondtal niet wordt weergegeven

$$ log(x) $$

is 10 het grondtal.

Het veranderen van het grondtal kan vrij eenvoudig, en is zeer nuttig als het grondtal van de log functie op je calculator niet gewijzigd kan worden

$$ log_2(8) = {log(8) \over log(2) } = { 0,903089987 \over 0,301029995 } = 3 $$

Decibels

De decibel is een op de logaritme gebaseerde rekeneenheid.
Zoals de cm een tiende deel is van de decimeter, is de 1 decibel een tiende deel van een Bel, 10 dB = 1 B.
In de radio techniek komen de waarde 3 dB en 6 dB vaak voor.

Als iets in dB's wordt aan gegeven is het een vergelijking. (Het is de toe cq afname).
De dB waarde is relatief.
Indien achter dB een aanduiding staat dan geeft dat een referentie waarde weer.

• dBm heeft als referentie waarde 1 mW (milliWatt),
• dBV heeft als referentie waarde 1 V,
• dBμV heeft als referentie waarde 1 microvolt.

Zodra er sprake is van een referentie waarde dan noemt men de dB waarde absoluut.

De formule bij het gebruik van vermogens:

$$ A = 10 • log { \left( Px \over Py \right ) } $$

.

Stijging in milliwatt t.o.v. 1 milliwatt	Van milliwatt naar decibel	Van decibel naar milliwatt
2 mW	10 * log(2/1) = 3 dB	10(3/10) = 2 mW
4 mW	10 * log(4/1) = 6 dB	10(6/10) = 4 mW
10 mW	10 * log(10/1) = 10 dB	10(10/10) = 10 mW
100 mW	10 * log(100/1) = 20 dB	10(20/10) = 100 mW
1000 mW	10 * log(1000/1) = 30 dB	10(30/10) = 1000 mW

Bij het terugrekenen kan in bovenstaande tabel het iets gemakkelijker door de decibels al te delen door tien dus ipv 10^(3/10) 10^(0,3).

De formules bij het gebruik van spanningen en stromen zijn :

$$ A = 20 • log { \left( u_1 \over u_2 \right ) } $$

en $$ A = 20 • log { \left( i_1 \over i_2 \right ) } $$

Stijging in volt t.o.v. 1 volt	Van voltage naar decibel	Van decibel naar voltage
2 V	20 * log(2/1) = 6 dB	10(6/20) = 2 V
4 V	20 * log(4/1) = 12 dB	10(12/20) = 4 V
10 V	20 * log(10/1) = 20 dB	10(20/20) = 10 V
100 V	20 * log(100/1) = 40 dB	10(40/20) = 100 V
1000 V	20 * log(1000/1) = 60 dB	10(60/20) = 1000 V

Als men log a schrijft, dan wordt daar mee altijd het grondtal 10 bedoeld. Derhalve moet men bij het terugrekenen bij het machtsverheffen van het grondtal 10 uitgaan.


De vermenigvuldingsfactor bij het berekenen van de decibel, is bij het terugrekenen de noemer bij het machtsverheffen.

Het getal pi

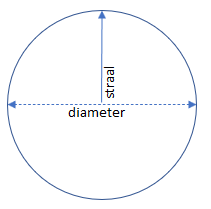Pi is de verhouding tussen omtrek en de diameter van een cirkel. Het symbool is $$ \pi $$ en de decimale getalswaarde is 3,141592653... Voor de meeste berekeningen is voldoende om 3,14 of 3,1416 aan te houden. De omtrek van een cirkel is : $$ \pi * $$ de diameter. En de omtrek van een cirkel is : 2 * de straal * $$ \pi $$

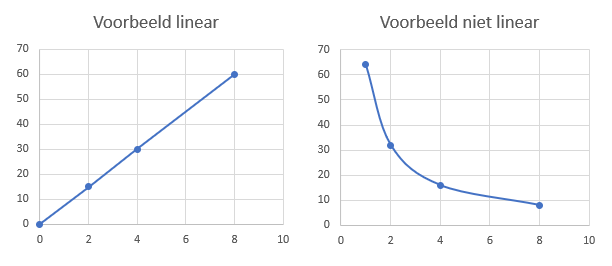
Interpretatie van lineaire en niet-lineaire grafieken

Binair getalstelsel

Het binaire talstelsel is een tweetallig stelsel. Om van binair om te rekenen naar decimaal, neemt men de meest linkse 1 om die vervolgens met deze positie minus 1 te gaan machtsverheffen. Zie onderstaande tabel voor de voorbeelden.

Binair	Decimaal	Van binair naar decimaal
0000	0	= 0
0001	1	= 20
0010	2	= 21
0011	3	= 21 + 20
0100	4	= 22
0101	5	= 22 + 20
0110	6	= 22 + 21
0111	7	= 22 + 21 + 20
1000	8	= 23
1001	9	= 23 + 20
1010	10	= 23 + 21
1011	11	= 23 + 21 + 20
1100	12	= 23 + 22
1101	13	= 23 + 22 + 20
1110	14	= 23 + 22 + 21
1111	15	= 23 + 22 + 21 + 20

Van decimaal naar binair kan op de volgende wijze;

Voorbeeld getal 13 naar binair omzetten;

13	dit is oneven noteer 1 en trek 1 van het decimale getal :	1
12	deel door 2 = 6 is even en noteer 0 :	01
6	deel door 2 = 3 dit is oneven noteer 1 en trek 1 van het decimale getal :	101
2	deel door 2 = 1 dit is oneven noteer 1 :	1101

Een oneven getal moet eerst even worden gemaakt voordat er gedeeld mag worden.

Voorbeeld getal 12 naar binair omzetten;

12	dit is even noteer 0 :	0
12	deel door 2 = 6 dit is even en noteer 0 :	00
6	deel door 2 = 3 dit is oneven noteer 1 en trek 1 van het decimale getal :	100
2	deel door 2 = 1 dit is oneven noteer 1	1100

Voorbeeld getal 57 naar binair omzetten;

57	dit is oneven noteer 1 en trek 1 van het decimale getal :	1
56	deel door 2 = 28 is even en noteer 0 :	01
28	deel door 2 = 14 is even en noteer 0 :	001
14	deel door 2 = 7 dit is oneven noteer 1 en trek 1 van het decimale getal :	1001
6	deel door 2 = 3 dit is oneven noteer 1 en trek 1 van het decimale getal :	11001
2	deel door 2 = 1 dit is oneven noteer 1 :	111001

• Vorige
• Terug
• Volgende

Referenties/bronnen:
VERON Leerboek voor de zend amateur
VRZA Cursus radio zend amateur
Wiki - Binair
Wiki - Decibel (eenheid)
Wiki - Decibel eenheid Geluid
Wiki - E_wiskunde
Wiki - Logaritmische
Wiki - Logaritmische_schaal